REAL 5.1 and 5.2 Exponential Functions and The Natural Exponential Function

Back again!

So with exponential functions, unlike with polynomial and linear functions, the constant term is the base and the exponent is the variable.

f(x)=a^x for every x in , where a>0 and a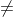1

as opposed to

This is the graph of :

The way to write an exponential function is

x is the exponential variable

b is the constant base

d is the horizontal asymptote (it will move the function up and down)

c will move the function left and right

a stretch or compress the graph, and is also the y-intercept.

when x=0 and c=0, =1, therefore the y-coordinate at x=0 wil be a (plus d of course)

if a=1, then the y intercept will always be 1 if d=0 and c=0 as well

when an exponential graph is to a negative power (or fraction, they're the same thing) then the graph is flipped horizontally

is the same as .

Here are some examples of solving exponential equations.

Another thing we learned about......

bumbumbumbumbumbumbumbumbumbumbumbum

dee dee dee dee daaaaa da daaaaa da daaaaaaaaaaaaa!!!!!!!!!!

Compound Interest Formula!!!!!!

A=present value

P=principal (initial value)

r=interest rate

n=#of compounding periods per year

t=#of years

I think all of this should be apparent. ;)

the only other thing that is really in 5.2 is not "e", but . looks much better.

is a magical number that somehow shows up in trees.

is the "natural number" and is very important. For those of you in APUSH, is the Ben Franklin of logarithms.

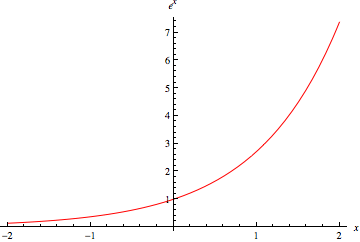
I hope you all had a great time, made fond memories, the natural exponential function is , and Good Night!!!