"Mr. Wilhelm imma let you finish, but David Mahoney had one of the best blog posts of ALL TIME."

-Kanye West

"When I was in school I didn't care about grades, I only cared about David's awesome blog post."

-Thad Wilhelm

"The times, they are a changin. And David Mahoney's blog post rules."

-Bob Dylan

"This blog post is winning!"

-Charles Sheen

"David Mahoney's blog post is cool."

-Albert Einstein, Abe Lincoln, Chuck Norris, Me, The Hoff, Superman, and everyone else

$4.1$

Now the math begins...

Chapter 4.1 was about Polynomial Functions of Degree Greater than 2... It was so much fun

So we'll start with the basics,

	with a positive leading coefficient	with a negative leading coefficient

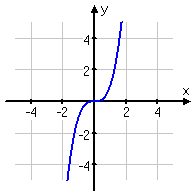
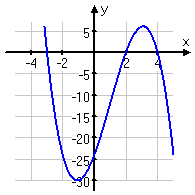
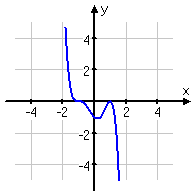
as you can see, while written in the form x^a, if "a" is positive both ends of the graph will go the same direction. ex: x^4=both ends point upwards & -x^4= both ends point downwards.

if the degree of the polynomial is negative then the ends go in different directions. BTW, the degree of a polynomial represents the highest degree of a polynominal's terms (with non-zero coefficent)

	with a positive leading coefficient	with a negative leading coefficient

I know what your probably telling yourself, "David you teach so well, I need to learn more" and I say you WILL have more!

Prepare yourself for... THE INTERMEDIATE VALUE THEOREM FOR POLYNOMIAL FUNCTIONS

Let a and b be real numbers such that a < b. If f is a polynomial function such that f(a)

and f(b) are opposite in sign, then there exists at least one zero in the interval [a, b].

Now, that's the intense smart people version. So let me brake it down for you.

***I tried to break it down and it was incredibly difficult so I'm gonna let you guys watch this video, I understand it after watching the video but it just takes too long to explain due to the complexity.***

http://homeworkhowto.com/intermediate-value-theorem/

http://www.calculus-help.com/the-intermediate-value-theorem/ <--- This is REALLY helpful

but the main focus of this chapter (on the homework at least) is graphing.

The graphing I can explain because it's easy when you think about it (I know thinking is hard but just try, okay?).

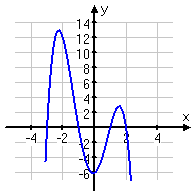
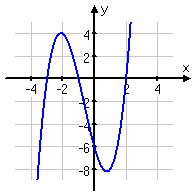
so we'll start with the polynomial f(x)=(x^3)-(3x^2)-9x+27

start by setting it equal to zero 0=(x^3)-(3x^2)-9x+27

0=(x^2)(x-3)(-9)(x-3)

0=((x^2)-9)(x-3)^2

so, the equation equals zero when x=3&(-3)

now, Wilhelm does the rest differently than I do because it's faster, but I like my way because it's easier.

first draw a number line and mark 3&(-3)

Then, plug in numbers between the placed intervals for x such as that there is one number used for each gap in the number line.

mark a "+" where the plugged in number for x makes the equation positive and a "-" where it makes it negative. Where the + and - signs are will tell you where your graph will be positive and where it will be negative.

start from the left, since the marking should be a - you will start below the axis, head up but stay below the x-axis until you've reached (-3). You will go above the axis now. If you haven't figured it out yet the graph will be staying above the axis once you've reached 3. But here's the tricky part. If you look back at the equation you'll notice 3 is an answer to (x-3)^2=0, since it's squared we treat it as a mini 2nd degree equation and make a parabola to keep the graph above the axis. In the end it looks like this:

If this looks close to your sketch then you done good, but if not then go through my very wordy explanation and hopefully you can figure it out.

wow that took a long time but I think I'm done.

I hope it wasn't that bad BYEEEE

ilovemath