4.3 Zeros of Polynomials ( The section of useless theorems)

It seems yet again that the wheel has chosen in my favor again and chose me last for blog post...so today in class we learned about the zeros of polynomials...and that this section, told by the legend himself, is full of useless theorems, because of this new technology called a calculator.  I will try to be "bubbly" during this post but there are no promises. There were a few that were of some importance.

Fundamental Theorem of Algebra- If a polynomial f(x) has positive degree and complex coefficients, then f(x) has at least one complex zero.  The first proof of this was done by Carl Friedrich Gauss...btw.

 Going back to stuff that really matters... So for those who don't understand be alarmed because I have no idea either, but luckily the internet had the answer.  This theorem in normal people terms means that for an nth degree polynomial there are n zeros ( I asked Eleni too and this is what she said and sense she is always right I'm going with this).


Next there was the Complete factorization theorem for polynomials that in many words basically says that in a polynomial -- a(x-c1)(x-c2).....(x-ck)... ck is a zero of f(x).



Now to ( again useless but interesting) Descartes' rule of signs....

<---Made by this man

(shout out to Hannah, he has a very spiffy top hat)














I'm not gonna quote the book ( so go read the thing yourself) but it means that for
(+) zeros equal the number of sign variation in f(x) ( the change in sign) or the number minus an even integer
(-) zeros equal the number of sign variations in f(-x) ( the change in sign) or the number minus and even integer.
Both of these are only for real numbers!!!

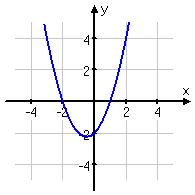
An example would be

f (x) = x⁵ – x⁴ + 3x³ + 9x² – x + 5               ( take f(x))

          ( count the number of sign changes) 



So in this there would be 4 or 2 positive real zeros.


f (–x) = (–x)⁵ – (–x)⁴ + 3(–x)³ + 9(–x)² – (–x) + 5    ( take f(-x))
= –x⁵ – x⁴ – 3x³ + 9x² + x + 5

                      ( count the number of sign changes)


So in this there would be 1 negative real zero.


And why does this all matter you say?!?! IT DOESN'T!! you see if you know how to graph or use this crazy tool called a calculator, this and many of the other theorems are very unnecessary.   


Next there are theorems about bounds which again don't matter...crazy....



Some of the homework problems had to do with finding a polynomial with prescribed zeros...which is pretty easy...

Find a polynomial f(x) of degree 3 that has the indicated zeros and satisfies the given condition...

Zeros= 2, -1, 3; f(1)= 5

Sense we know that the polynomial has a degree of 3 we know that
f(x)= a(x-2)(x+1)(x-3)

to find a we plug in f(1)=5  then solve for a

5=a(1-2)(1+1)(1-3)
5=a(-1)(2)(-2)
5=a(4)
5/4=a  (don't yell at me Mr.Wilhelm for not using the thingy to make that proper cuz the thingy didn't work)
so f(x)= 5/4(x-2)(x+1)(x-3)   So simply and you get
f(x)= 5/4x^3-5x^2+5/4x+15/2


So that's all that we "learned".... even though it wasn't necessary so some of this blog was a waste of time....but oh well... and if you still don't get math....join the club

Long Live King Thaddeus

And remember kids, teaching chemistry is more fun because in there things explode and you can't do that in math.
Most awesomest video ever 

Jennifer Kendall (5th hour FTW)


And i have lost the game

"Mr. Wilhelm imma let you finish, but David Mahoney had one of the best blog posts of ALL TIME."

-Kanye West

"When I was in school I didn't care about grades, I only cared about David's awesome blog post."

-Thad Wilhelm

"The times, they are a changin. And David Mahoney's blog post rules."

-Bob Dylan

"This blog post is winning!"

-Charles Sheen

"David Mahoney's blog post is cool."

-Albert Einstein, Abe Lincoln, Chuck Norris, Me, The Hoff, Superman, and everyone else

$4.1$

Now the math begins...

Chapter 4.1 was about Polynomial Functions of Degree Greater than 2... It was so much fun

So we'll start with the basics,

	with a positive leading coefficient	with a negative leading coefficient

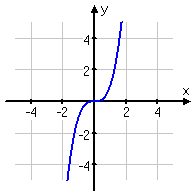
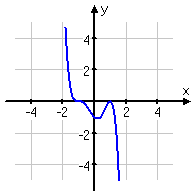
as you can see, while written in the form x^a, if "a" is positive both ends of the graph will go the same direction. ex: x^4=both ends point upwards & -x^4= both ends point downwards.

if the degree of the polynomial is negative then the ends go in different directions. BTW, the degree of a polynomial represents the highest degree of a polynominal's terms (with non-zero coefficent)

	with a positive leading coefficient	with a negative leading coefficient

I know what your probably telling yourself, "David you teach so well, I need to learn more" and I say you WILL have more!

Prepare yourself for... THE INTERMEDIATE VALUE THEOREM FOR POLYNOMIAL FUNCTIONS

Let a and b be real numbers such that a < b. If f is a polynomial function such that f(a)

and f(b) are opposite in sign, then there exists at least one zero in the interval [a, b].

Now, that's the intense smart people version. So let me brake it down for you.

***I tried to break it down and it was incredibly difficult so I'm gonna let you guys watch this video, I understand it after watching the video but it just takes too long to explain due to the complexity.***

http://homeworkhowto.com/intermediate-value-theorem/

http://www.calculus-help.com/the-intermediate-value-theorem/ <--- This is REALLY helpful

but the main focus of this chapter (on the homework at least) is graphing.

The graphing I can explain because it's easy when you think about it (I know thinking is hard but just try, okay?).

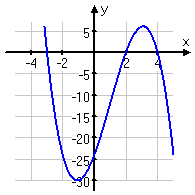
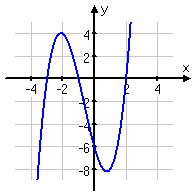
so we'll start with the polynomial f(x)=(x^3)-(3x^2)-9x+27

start by setting it equal to zero 0=(x^3)-(3x^2)-9x+27

0=(x^2)(x-3)(-9)(x-3)

0=((x^2)-9)(x-3)^2

so, the equation equals zero when x=3&(-3)

now, Wilhelm does the rest differently than I do because it's faster, but I like my way because it's easier.

first draw a number line and mark 3&(-3)

Then, plug in numbers between the placed intervals for x such as that there is one number used for each gap in the number line.

mark a "+" where the plugged in number for x makes the equation positive and a "-" where it makes it negative. Where the + and - signs are will tell you where your graph will be positive and where it will be negative.

start from the left, since the marking should be a - you will start below the axis, head up but stay below the x-axis until you've reached (-3). You will go above the axis now. If you haven't figured it out yet the graph will be staying above the axis once you've reached 3. But here's the tricky part. If you look back at the equation you'll notice 3 is an answer to (x-3)^2=0, since it's squared we treat it as a mini 2nd degree equation and make a parabola to keep the graph above the axis. In the end it looks like this:

If this looks close to your sketch then you done good, but if not then go through my very wordy explanation and hopefully you can figure it out.

wow that took a long time but I think I'm done.

I hope it wasn't that bad BYEEEE

ilovemath

3.7 Operations on Functions

This section is focused on adding, subtracting, etc. with functions. Sounds easy right? Well it is. Kinda.

Let's start with addition. We are going to use the functions and .

We are going to add them by saying , which is equal to .

So let's add:

1. 
2. 
3. 

So we have =

Then we plug in x, and find an answer.

The process is the same for , , and .

But when it comes to division, we have to make sure the denominator isn't zero.

But you have to remember: use parentheses when doing these operations. Or the world will crumble. And it will be YOUR fault.

Now it gets freaky. We got these things called Composite Functions.

They are written as . The little circle icon () is the composition sign. It is read "f

composed with g of x." It means you take and plug it into function .

So it is also written as .

If =2x, and =3x,+2, you take 2x and substitute it for x. So =6x+2.

Well, that's really all we've learned about operations on functions. Byeeee

Andrew Geller

3.6 Quadratic Functions

QUADRATIC FUNCTIONS WOOOO PARTYYY

Let's start off with the quadratic formula.

or

because y is a function of x

A function f is a quadratic function if

The graph of a quadratic function is a parabola.

• is a parabola with vertex at the origin (0,0)
• has a vertical axis
• opens upward if a>0 and downward if a<0

the quadratic function

can be obtained by vertical and/or horizontal shifts of the graph:

Some things observed from a quadratic equation:

• c is the y-intercept
• set y=0 and solve to get x-intercepts
• a>0 open upwards
• a<0 open downwards
• a tells to what extreme the parabola is vertically stretched or compressed. the larger the number, the more extremely it is vertically stretched
• b=0 if axis of symmetry is the y-axis
• b is a vertical line; it serves as the axis of symmetry, splitting the parabola in two at the vertex
• to find the vertex of a parabola solve for the x-coordinate and then plug in the value to solve for the y coordinate

A quadratic formula can also be expressed in the form

this is known as the standard equation of a parabola with vertical axis

to reach this form of an equation from the quadratic formula you complete the square

ex:

given

factor out 3

complete the square for

is the equivelant equation in form

when an equation is in this form its has a vertex (h,k) and depending on a being > or < than 0, (h,k) will be the minimum value or the maximum value

Finding an equation of a parabola with a given vertex ex:

find an equation of a parabola that has

vertex(2,3)

vertical axis

passes through the point (5,1)

we will try to put the parabola in form

vertex (3,2) gives us h=2 and k=3

plug in the coordinate (5,1) because we know it is on the parabola

solve to get that

the videos and pictures wont post...sorry guys